Java中的小数运算与精度丢失问题 (BigDecimal详解使用以及RoundingMode舍入模式说明)

崧峻
原创
发布时间: 2025-08-23 17:25:55 | 阅读数 0收藏数 0评论数 0
编码
金额精度问题
小数精度
BigDecimal
舍入模式
封面
在实际开发中，尤其是金融、电商、支付等场景，金额计算往往要求 绝对精确。然而，Java 中常用的 double 或 float 由于采用二进制浮点数表示，无法精确表示某些十进制小数，比如 0.1、0.2，这会导致 0.1 + 0.2 != 0.3 这样的问题。如果直接用浮点数处理金额，可能出现汇总误差、四舍五入错误，进而影响业务结果。本文将通过示例代码演示 BigDecimal 的创建方式、加减乘除运算，以及不同舍入模式在金额计算中的实际效果，帮助开发者在真实项目中正确处理涉及金钱和高精度计算的业务逻辑。
1

问题出现

图片

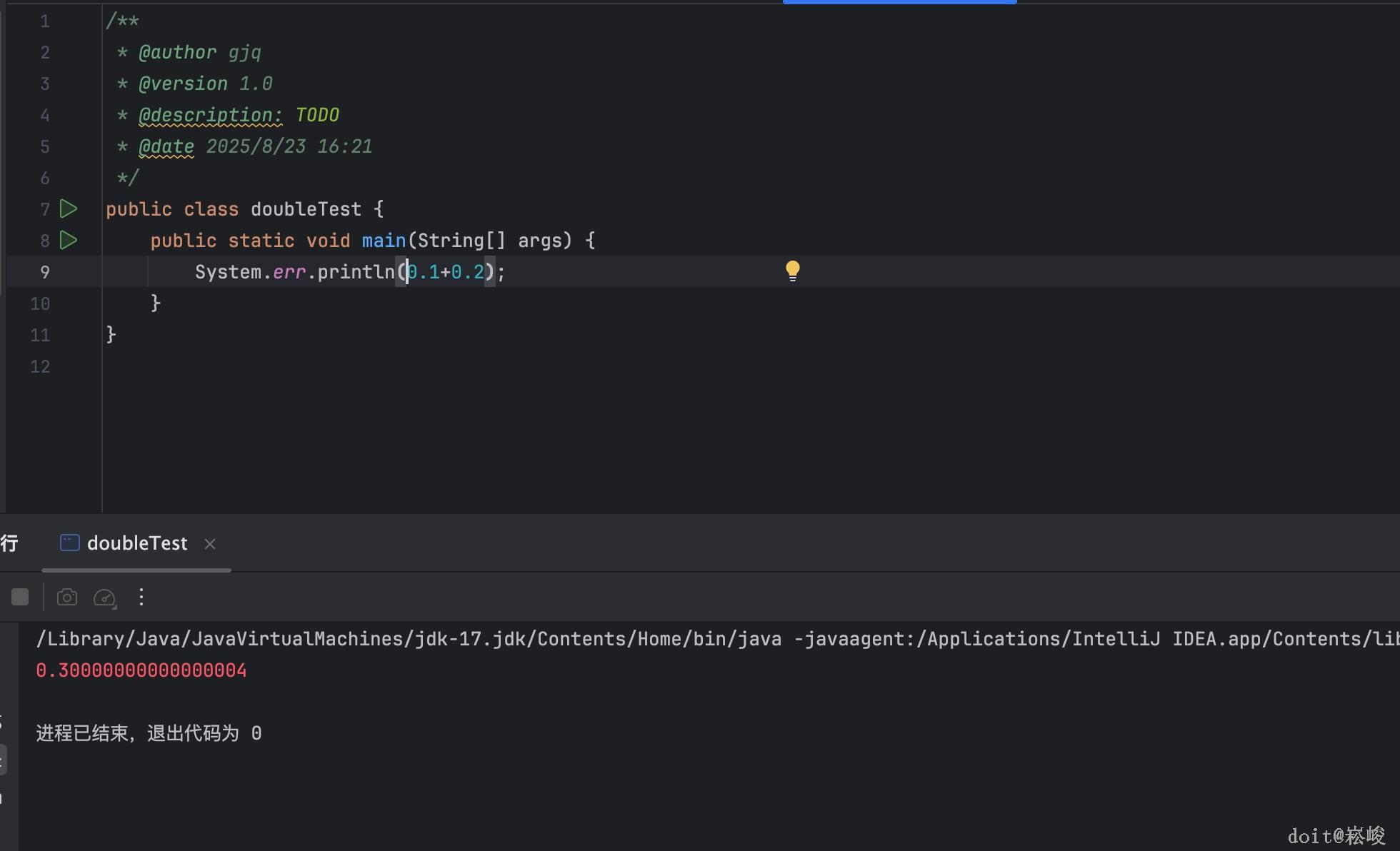
如图所示 0.1+0.2是不为0.3的，那么这是为什么呢？


2

原因？

图片

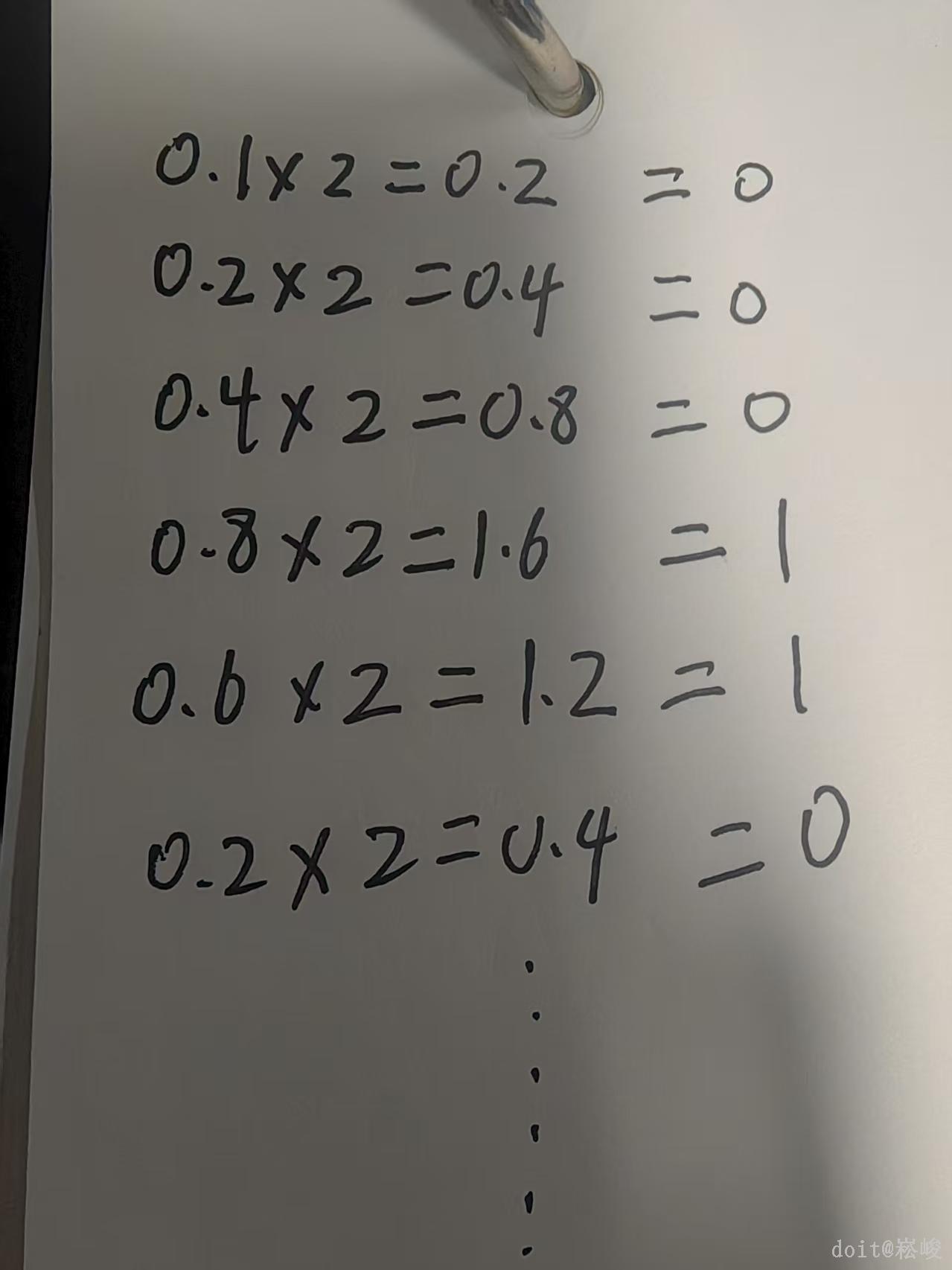
Java 中的浮点数本质

在 Java 里，0.1、0.2、0.3 默认是 double 类型（双精度浮点数）。

浮点数用二进制小数来表示，而有些十进制小数（比如 0.1 和 0.2）在二进制里是 无限循环小数，不能被精确表示。

举个例子：

  1. 十进制 0.1 → 二进制是 0.0001100110011001100...（无限循环）
  2. 十进制 0.2 → 二进制是 0.0011001100110011001...（无限循环）

存储时只能 截断，所以：

  1. 0.1 实际存储为二进制接近 0.10000000000000000555
  2. 0.2 实际存储为二进制接近 0.20000000000000001110


十进制小数转换为二进制小数 如图2

十进制小数转换成二进制小数采用"乘2取整，顺序排列"法。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数 部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。

然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。


所以，计算机无法精确的表示出0.1的二进制数，它只能表示一个非常接近0.1但又不等于0.1的一个数，到这里应该就能大致理解，为什么0.1+0.2!=0.3了

3

什么是BigDecimal?

图片

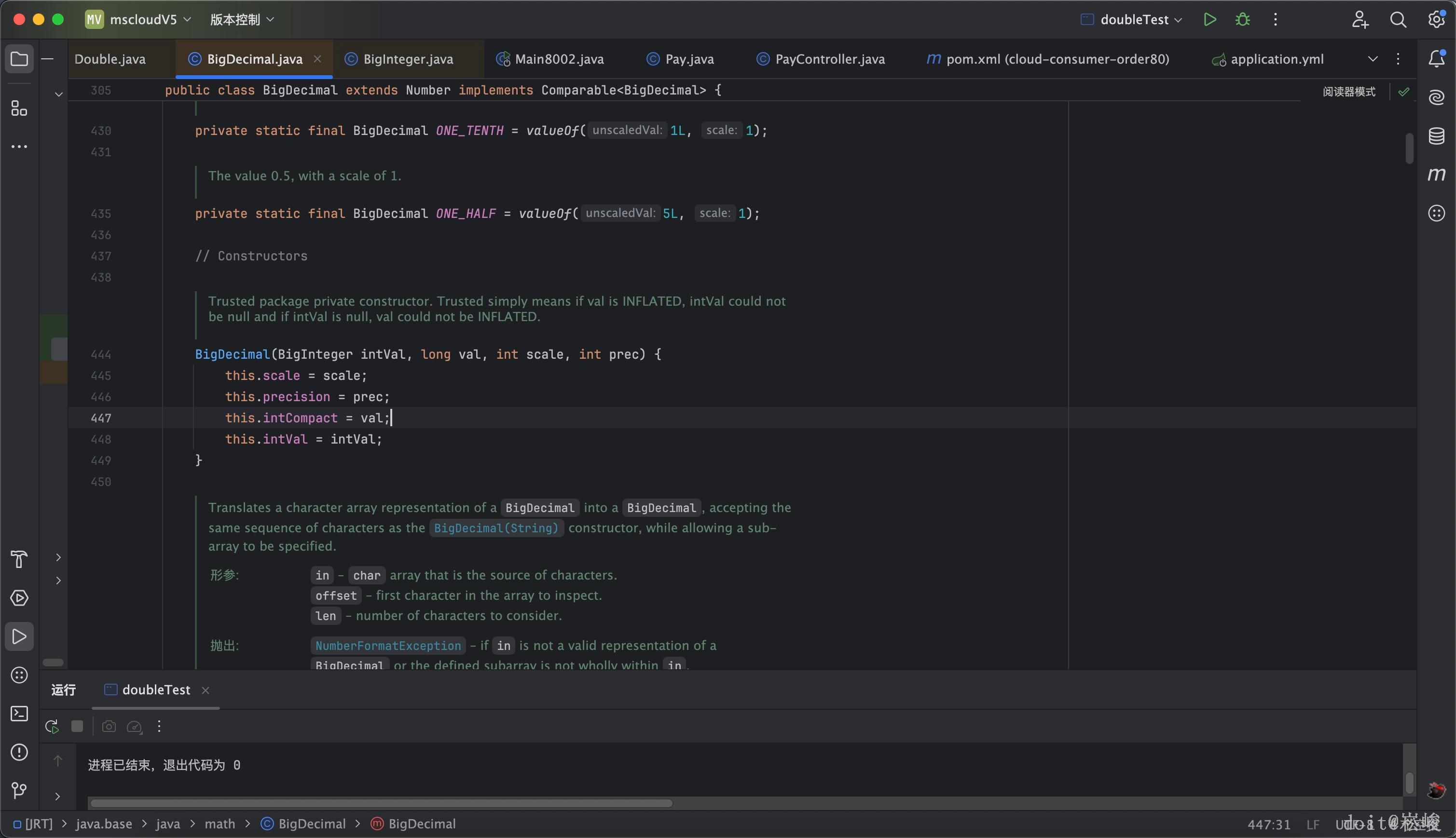
BigDecimal 是 Java 提供的任意精度的定点小数类（在 java.math 包里）。

它不像 double 那样使用二进制浮点数，而是直接用 十进制表示 存储数据，因此可以做到 精确表示任意大小和任意精度的小数。


BigDecimal = 任意精度整数 (unscaledValue) + 小数位数 (scale)，通过十进制存储和运算来避免 double 的精度误差，适合高精度和大数计算。


4

BigDecimal 如何使用

图片
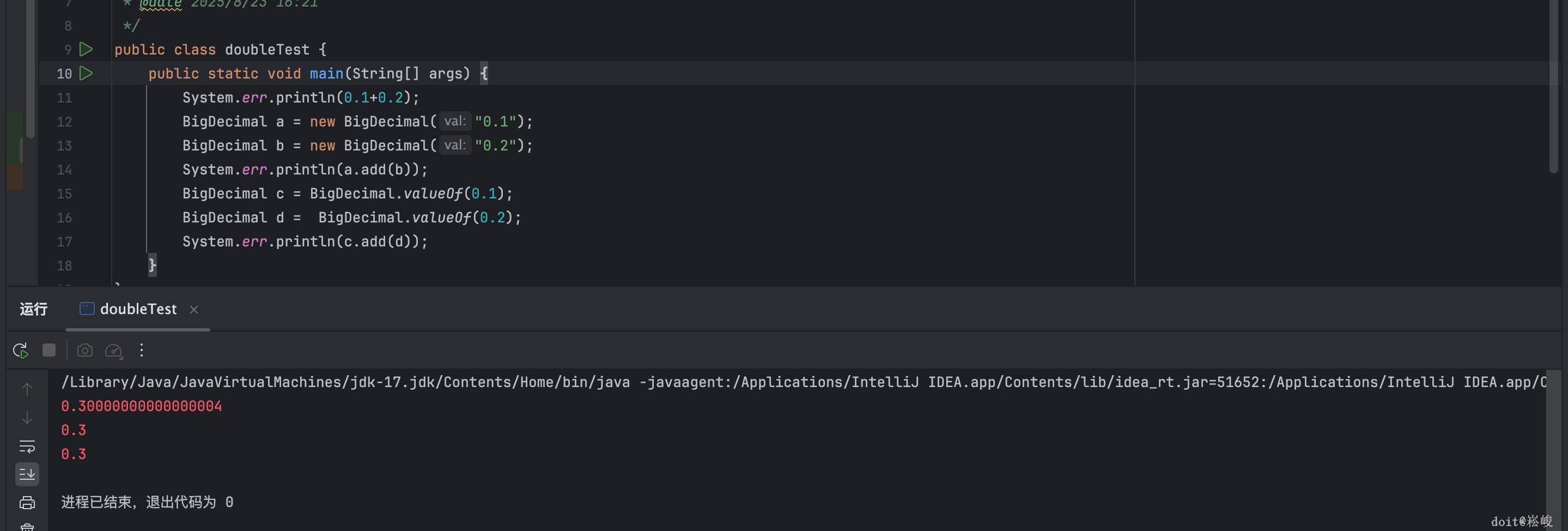
BigDecimal a = new BigDecimal("0.1");
BigDecimal b = new BigDecimal("0.2");
System.err.println(a.add(b));
BigDecimal c = BigDecimal.valueOf(0.1);
BigDecimal d = BigDecimal.valueOf(0.2);
System.err.println(c.add(d));


如上面所示这两种方式 new BigDecimal(0.2); 千万不要这种写法 因为这样的话 数值的精度就已经丢失了

5

基础使用

图片

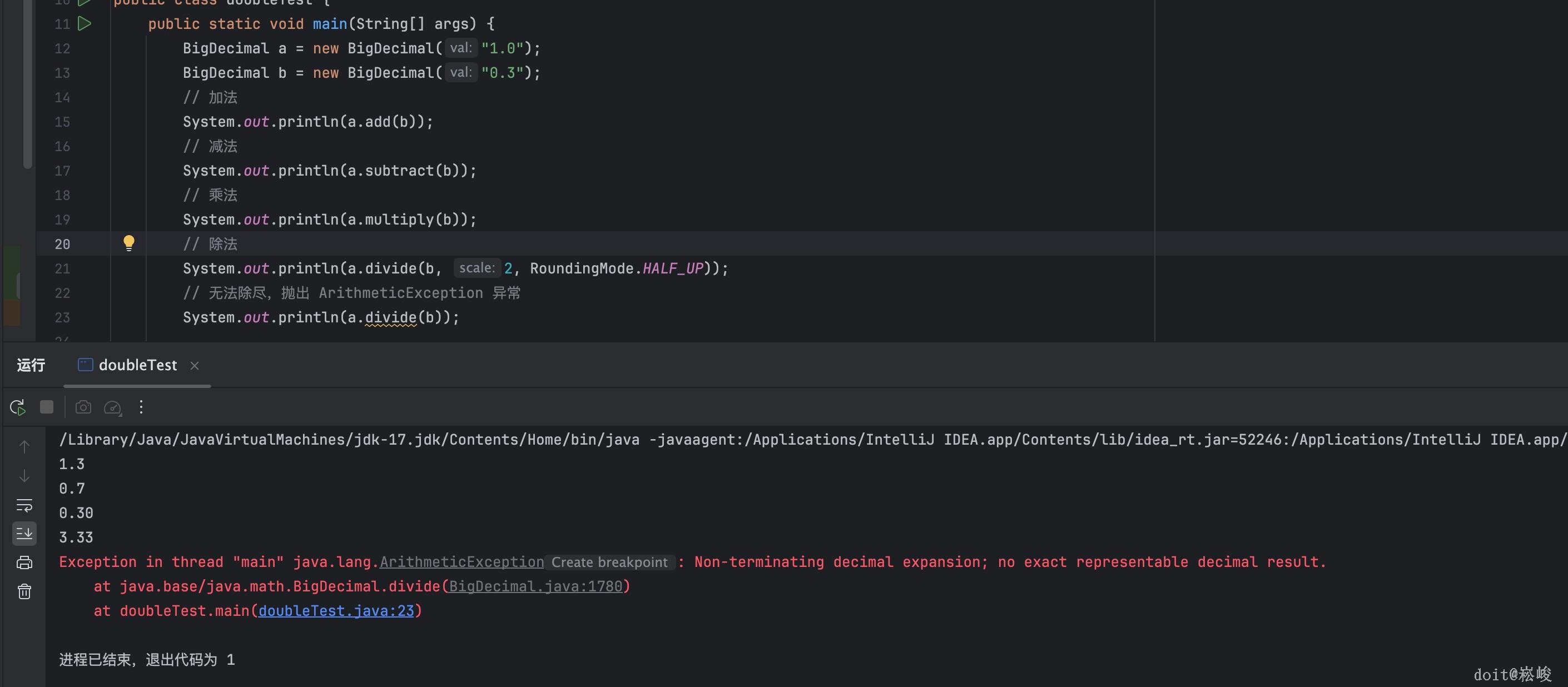
如图1所示的加减乘除的案例

  1. add 方法用于将两个 BigDecimal 对象相加，
  2. subtract 方法用于将两个 BigDecimal 对象相减。
  3. multiply 方法用于将两个 BigDecimal 对象相乘，
  4. divide 方法用于将两个 BigDecimal 对象相除。(第一个参数是除谁，第二个参数是保留几位小数，第三个参数是舍入模式) -> 舍入模式在下一步详细说了一下


6

除法 RoundingMode 舍入模式说明

图片
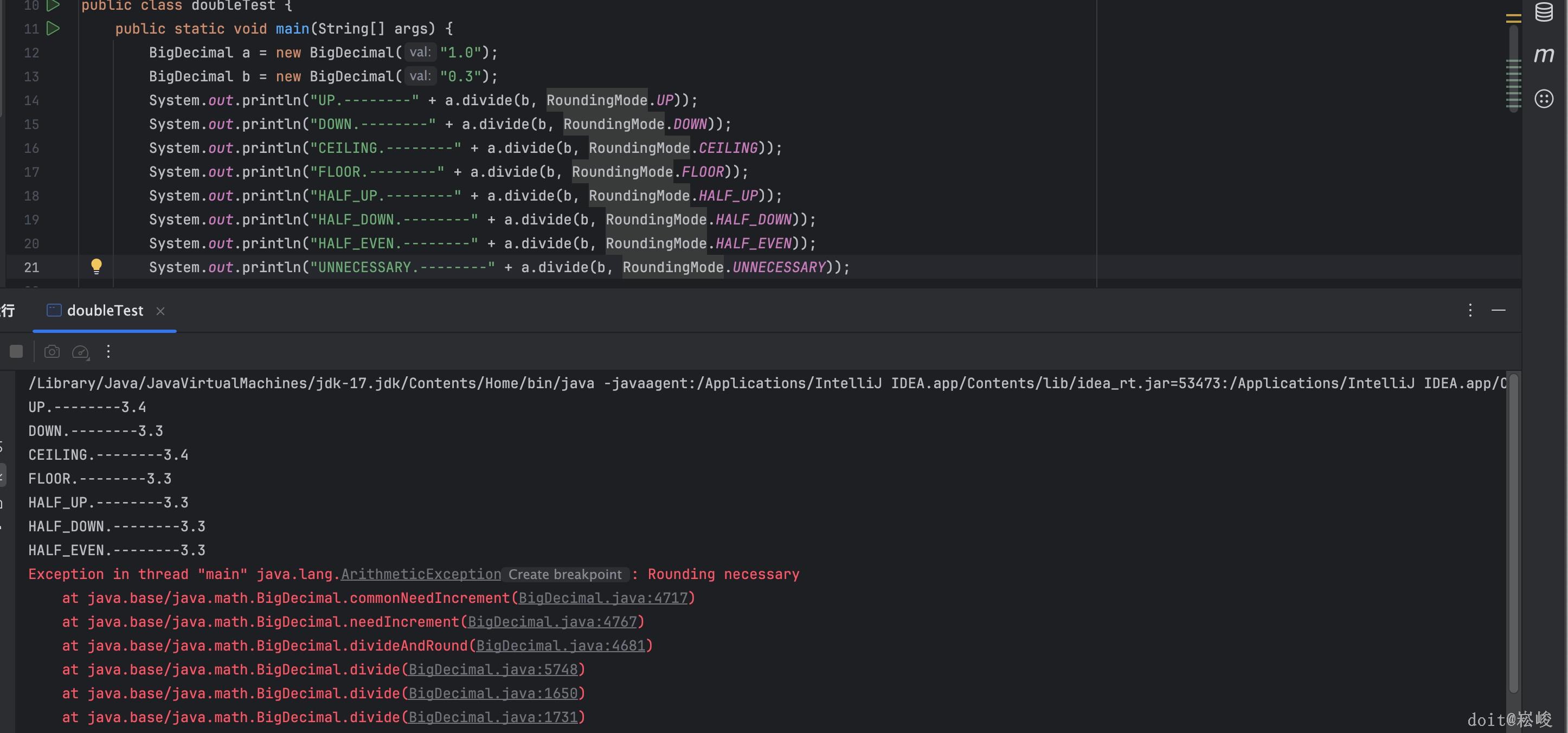
java.math.RoundingMode：这是一种枚举类型，它定义了8种数据的舍入模式。它与java.math.BigDecimal类中定义的8个同名静态常量的作用相同，可用BigDecimal.setScale(int newScale, RoundingMode roundingMode)来设置数据的精度和舍入模式。

RoundingMode 含义与示例

  1. UP（远离 0 舍入）
  2. 定义：只要有被截断的小数，就朝远离 0 的方向进一。
  3. 例：1.234 → (保留2位) 1.24；-1.231 → -1.24
  4. DOWN（趋向 0 舍入，截断）
  5. 定义：直接截断到指定位数，始终向 0 靠。
  6. 例：1.239 → 1.23；-1.239 → -1.23
  7. CEILING（向正无穷大）
  8. 定义：结果向 +∞ 方向靠拢；对正数类似 UP、对负数类似 DOWN。
  9. 例：1.231 → 1.24；-1.231 → -1.23
  10. FLOOR（向负无穷大）
  11. 定义：结果向 −∞ 方向靠拢；对正数类似 DOWN、对负数类似 UP。
  12. 例：1.239 → 1.23；-1.231 → -1.24
  13. HALF_UP（四舍五入）
  14. 定义：离两侧等距（.5）时，朝远离 0 的一侧进一。
  15. 例：1.235 → 1.24；-1.235 → -1.24
  16. HALF_DOWN（五舍六入）
  17. 定义：一般向最接近的值；遇到 .5 时，朝 0 的方向舍去。
  18. 例：1.235 → 1.23；-1.235 → -1.23
  19. HALF_EVEN（银行家舍入）
  20. 定义：一般向最接近；遇到 .5，看保留位的前一位：奇数进一、偶数不进（使结果末位变成偶数）。
  21. 例：1.235 → 1.24（3 为奇数，进一成 4）；1.245 → 1.24（4 为偶数，不进）
  22. UNNECESSARY（不允许需要舍入）
  23. 定义：要求结果本来就能精确表示（无需舍入），否则抛 ArithmeticException。


案例如图所示

7

工具类

图片
import java.math.BigDecimal;
import java.math.RoundingMode;

/**
* 简化BigDecimal计算的小工具类
*/
public class BigDecimalUtil {

/**
* 默认除法运算精度
*/
private static final int DEF_DIV_SCALE = 10;

private BigDecimalUtil() {
}

/**
* 提供精确的加法运算。
*
* @param v1 被加数
* @param v2 加数
* @return 两个参数的和
*/
public static double add(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.add(b2).doubleValue();
}

/**
* 提供精确的减法运算。
*
* @param v1 被减数
* @param v2 减数
* @return 两个参数的差
*/
public static double subtract(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.subtract(b2).doubleValue();
}

/**
* 提供精确的乘法运算。
*
* @param v1 被乘数
* @param v2 乘数
* @return 两个参数的积
*/
public static double multiply(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.multiply(b2).doubleValue();
}

/**
* 提供（相对）精确的除法运算，当发生除不尽的情况时，精确到
* 小数点以后10位，以后的数字四舍六入五成双。
*
* @param v1 被除数
* @param v2 除数
* @return 两个参数的商
*/
public static double divide(double v1, double v2) {
return divide(v1, v2, DEF_DIV_SCALE);
}

/**
* 提供（相对）精确的除法运算。当发生除不尽的情况时，由scale参数指
* 定精度，以后的数字四舍六入五成双。
*
* @param v1 被除数
* @param v2 除数
* @param scale 表示表示需要精确到小数点以后几位。
* @return 两个参数的商
*/
public static double divide(double v1, double v2, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.divide(b2, scale, RoundingMode.HALF_EVEN).doubleValue();
}

/**
* 提供精确的小数位四舍六入五成双处理。
*
* @param v 需要四舍六入五成双的数字
* @param scale 小数点后保留几位
* @return 四舍六入五成双后的结果
*/
public static double round(double v, int scale) {
if (scale < 0) {
throw new IllegalArgumentException(
"The scale must be a positive integer or zero");
}
BigDecimal b = BigDecimal.valueOf(v);
BigDecimal one = new BigDecimal("1");
return b.divide(one, scale, RoundingMode.HALF_UP).doubleValue();
}

/**
* 提供精确的类型转换(Float)
*
* @param v 需要被转换的数字
* @return 返回转换结果
*/
public static float convertToFloat(double v) {
BigDecimal b = new BigDecimal(v);
return b.floatValue();
}

/**
* 提供精确的类型转换(Int)不进行四舍六入五成双
*
* @param v 需要被转换的数字
* @return 返回转换结果
*/
public static int convertsToInt(double v) {
BigDecimal b = new BigDecimal(v);
return b.intValue();
}

/**
* 提供精确的类型转换(Long)
*
* @param v 需要被转换的数字
* @return 返回转换结果
*/
public static long convertsToLong(double v) {
BigDecimal b = new BigDecimal(v);
return b.longValue();
}

/**
* 返回两个数中大的一个值
*
* @param v1 需要被对比的第一个数
* @param v2 需要被对比的第二个数
* @return 返回两个数中大的一个值
*/
public static double returnMax(double v1, double v2) {
BigDecimal b1 = new BigDecimal(v1);
BigDecimal b2 = new BigDecimal(v2);
return b1.max(b2).doubleValue();
}

/**
* 返回两个数中小的一个值
*
* @param v1 需要被对比的第一个数
* @param v2 需要被对比的第二个数
* @return 返回两个数中小的一个值
*/
public static double returnMin(double v1, double v2) {
BigDecimal b1 = new BigDecimal(v1);
BigDecimal b2 = new BigDecimal(v2);
return b1.min(b2).doubleValue();
}

/**
* 精确对比两个数字
*
* @param v1 需要被对比的第一个数
* @param v2 需要被对比的第二个数
* @return 如果两个数一样则返回0，如果第一个数比第二个数大则返回1，反之返回-1
*/
public static int compareTo(double v1, double v2) {
BigDecimal b1 = BigDecimal.valueOf(v1);
BigDecimal b2 = BigDecimal.valueOf(v2);
return b1.compareTo(b2);
}

}
阅读记录0
点赞0
收藏0
禁止 本文未经作者允许授权，禁止转载
更多相关项目
猜你喜欢
评论/提问(已发布 0 条)
评论 评论
收藏 收藏
分享 分享
pdf下载 下载